Overstromingsfrequentiecurves, die worden gebruikt om waterkeringen te ontwerpen, worden gebaseerd op relatief korte datasets van jaarlijks gemeten maximale afvoeren. Door de datareeks uit te breiden met historische overstromingen kan een overstromingsfrequentieanalyse uitgevoerd worden met minder onzekerheid.
Download hier de pdf van dit artikel
Geschreven door Anouk Bomers (Universiteit Twente), Ralph Schielen (Rijkswaterstaat en Universiteit Twente, nu Rijkswaterstaat en TU Delft), Suzanne Hulscher (Universiteit Twente)
Overstromingen leiden elk jaar opnieuw tot slachtoffers en grote schade over de hele wereld. Hoewel de laatste grote rivieroverstroming in Nederland dateert uit 1926, toonden de hoogwaters in 1993 en 1995 wederom het belang van voldoende hoge en sterke dijken aan. Het is dan ook belangrijk dat waterkeringen ontworpen worden volgens een veiligheidsnormering die recht doet aan de te beschermen bevolking en de economische waarde achter de dijken.
De veiligheidsnormen die worden gehanteerd bij het ontwerpen van waterkeringen om het achterland te beschermen tegen ernstige overstromingen, zijn vaak gebaseerd op een statistische herhalingstijd. In Europa worden overstromingsfrequentieanalyses uitgevoerd om de afvoeren te schatten die horen bij verschillende herhalingstijden.
Deze analyses zijn eenvoudig uit te voeren: een kansverdelingsfunctie wordt opgesteld met behulp van een dataset van jaarlijkse maximale afvoerwaarnemingen. In Nederland worden afvoeren van de Rijn bij Lobith gemeten sinds 1901. Dit resulteert in een dataset van 118 jaar aan jaarlijkse maximale afvoeren. Voor het ontwerp van waterkeringen worden vaak grote herhalingstijden, bijvoorbeeld eens in de 1.250 of 10.000 jaar, gebruikt.
Een groot nadeel van deze methode met een relatief korte reeks is dat voor het afleiden van zulke grote herhalingstijden extrapolatie nodig is. Dit gaat gepaard met grote onzekerheden. Deze onzekerheid kan verkleind worden door de dataset van gemeten afvoeren uit te breiden met historische overstromingen. In dit artikel wordt gepresenteerd hoe historische overstromingen van de Rijn kunnen helpen om de onzekerheid in de frequentieanalyse en daarmee in het ontwerp van toekomstige waterkeringen te verkleinen.
Gemeten dataset bij Lobith
De Rijn ontspringt in de Zwitserse Alpen, stroomt door Duitsland stroomt en komt bij Lobith Nederland binnen (zie afbeelding 1). Het doel van deze studie is om de dataset van jaarlijkse maximale afvoeren bij Lobith uit te breiden met historische overstromingen.
Alhoewel afvoermetingen bij Lobith worden uitgevoerd sinds 1901, worden waterstanden al gemeten sinds 1866. Daarnaast zijn er van de omliggende meetlocaties Emmerich, Pannerden en Nijmegen waterstandsmetingen beschikbaar vanaf 1772. Deze waterstandsmetingen zijn door Toonen [1] gebruikt om bijbehorende afvoeren bij Lobith te bepalen met behulp van een lineaire regressieanalyse.
Dit resulteert in een continue dataset voor de periode 1772-2018. Deze dataset kan worden uitgebreid met historische overstromingen die helemaal terug gaan tot het jaar 1300. Dit resulteert in een datareeks met een lengte van ongeveer 700 jaar.
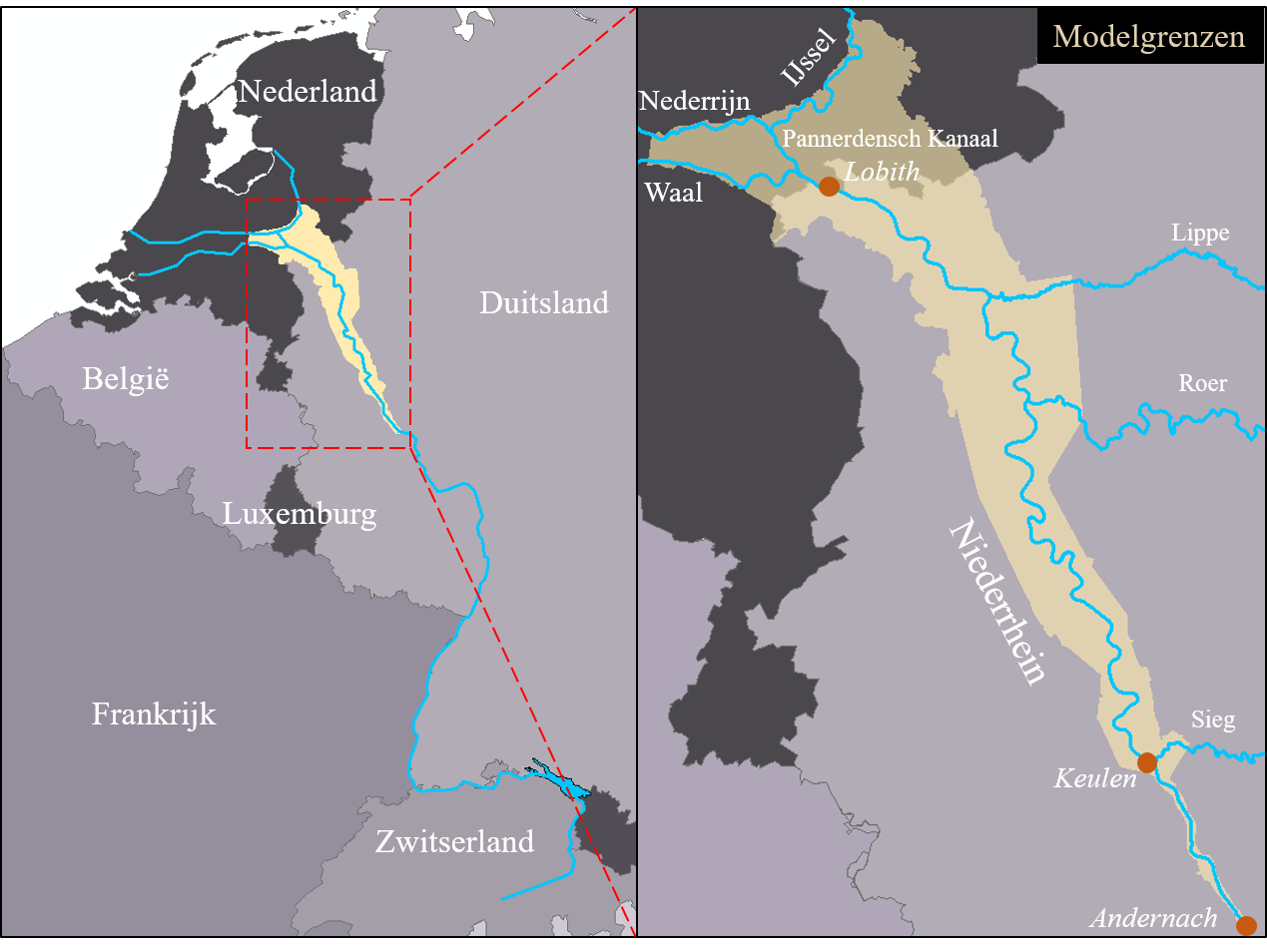
Afbeelding 1. Studiegebied, met in geel gearceerd de modelgrenzen van het 1D-2D gekoppeld hydraulisch model. Het hydraulische model wordt gebruikt om de huidige gevolgen van de historische overstromingen bij Keulen te simuleren
Methode
Historische overstromingen
Historische bronnen, zoals krantenartikelen, schilderijen en dagboeken, met informatie over overstromingen van de Rijn gaan terug tot de twaalfde eeuw [2]. Herget en Meurs [3] hebben zulke historische bronnen verzameld om inzicht te krijgen in de ernst van overstromingen van de Rijn nabij Keulen.
Deze inzichten hebben ze gebruikt om de maximale waterstanden tijdens de hoogwaters te reconstrueren. Met deze waterstanden kon vervolgens bijbehorende maximale afvoeren bepaald worden aan de hand van een reconstructie van de rivierbathymetrie (de ligging en dwarssnedes van de rivier) en een schatting van de bodemruwheid.
In totaal hebben Herget en Meurs twaalf overstromingen gereconstrueerd in de periode voor 1772 met de oudste overstroming in 1342. De overige overstromingen vonden plaats in 1374, 1496, 1497, 1535, 1595, 1651, 1682, 1740, 1753 en 1758. Al deze overstromingen werden veroorzaakt door een grote hoeveelheid neerslag. Overige overstromingen (bijvoorbeeld opstuwing van de waterstand door ijsdammen) zijn niet meegenomen, aangezien afvoer-waterstandsrelaties in deze gevallen geen nauwkeurige schatting van de opgetreden maximale afvoer geven.Hier ga je verder met je Vakartikel. Deze tekst wordt afgebeeld in 14 punten. Gebruik 'enter' om naar een volgend tekstblok te gaan.
De overstroming van 1342 is erg bijzonder, omdat deze in de zomer plaatsvond. Een hevig regenfront teisterde centraal-Duitsland in de maand juli. Dit leidde tot overstromingen in het stroomgebied van de Rijn. Er zijn erg veel historische bronnen beschikbaar die een beeld geven van de ernst van de overstromingen. Sommige bronnen zijn echter tegenstrijdig. Dit komt waarschijnlijk doordat er in het jaar 1342 drie hoogwaters hebben plaatsgevonden, namelijk in februari, veroorzaakt door ijsdammen, in april door smeltende sneeuw in de Alpen en dat in juli door hevige regenbuien [4].
De overstromingen in juli waren het extreemst en zorgden voor schade aan bruggen en gebouwen. Met name de gevolgen nabij Keulen zijn erg goed gedocumenteerd. Met behulp van deze informatie waren Herget en Meurs in staat om een schatting te maken van de maximale waterstand die optrad tijdens deze gebeurtenis. Met behulp van deze waterstand kon vervolgens een schatting gemaakt worden van de piek in de afvoerverdeling van dit hoogwater.
De grootste overstroming van de afgelopen 1.000 jaar heeft, zo lijkt het, in 1374 plaatsgevonden. Hevige regenbuien veroorzaakten hoogwaters rond 6 en 25 januari en rond 10 februari. Vanwege de extreem hoge waterstanden tijdens deze overstromingen, zijn er erg veel historische bronnen beschikbaar. Sommige bronnen zeggen dat het zelfs mogelijk was om over de stadsmuren van Keulen heen te varen. Dit soort informatie geeft inzicht in de opgetreden maximale waterstand.

Afbeelding 2. Waterstandspijlen nabij Rees, Duitsland. Foto: Anouk Bomers
Normaliseren historische afvoeren
Om de tijdsreeks van jaarlijkse maximale afvoeren bij Lobith uit te kunnen breiden, moet achterhaald worden welke afvoer bij Lobith nu zou optreden als gevolg van elk van de twaalf gereconstrueerde historische hoogwaterstanden bij Keulen. Het riviersysteem is namelijk erg veranderd in de afgelopen eeuwen.
Zo zijn de dijken langs de Niederrhein aanzienlijk verhoogd. Door de dijkverhogingen kan er meer water richting Lobith stromen. Daarom zijn we niet geïnteresseerd in de historische maximale afvoeren bij Lobith, maar de maximale afvoeren die op dit moment zullen optreden als bij Keulen een hoogwater optreedt van dezelfde omvang als van een historische gebeurtenis.
Om te achterhalen welke afvoer bij Lobith zal optreden als gevolg van de historische overstromingen bij Keulen is gebruik gemaakt van een gekoppeld 1D-2D hydraulisch model. In dit model zijn het zomer- en winterbed geschematiseerd met 1D-profielen en de bedijkte gebieden met een 2D-grid. Een 2D-grid is nodig om de overstromingspatronen in het achterland correct te simuleren [5]. De modelgrenzen zijn weergegeven in afbeelding 1.
Om een groot scala aan potentiële overstromingsscenario’s door te kunnen rekenen, inclusief potentiële dijkdoorbaken, is een Monte Carlo-analyse uitgevoerd. Hierbij worden verschillende scenario’s doorgerekend, elk met andere startcondities. Het resultaat van deze verzameling simulaties geeft het scala van mogelijke uitkomsten weer. In deze analyse zijn de volgende onzekere parameters meegenomen als random input parameters. Deze bepalen de startcondities van een simulatie (afbeelding 3):
- De maximale afvoer bij Keulen. De historische reconstructies van Herget en Meurs gingen gepaard met grote onzekerheden. Zo is de bathymetrische reconstructie van de rivier onzeker, net als de bodemruwheid. Deze onzekerheden leiden tot een grote bandbreedte aan potentiële maximale afvoeren voor elk van de twaalf historische overstromingen (afbeelding 4).
- De golfvorm. Niet alleen de maximale afvoer is onzeker, maar ook de golfvorm. Daarom is deze in de Monte Carlo-analyse gevarieerd. Er is gebruik gemaakt van een dataset van 250 golfvormen die kunnen optreden onder het huidige klimaat [6]. Op deze manier kan een grote variëteit aan potentiele afvoergolven in de analyse meegenomen worden, namelijk: afvoergolven met een spitse piek, een brede piek of twee pieken. Voor elke Monte Carlorun wordt een afvoergolf willekeuring getrokken en geschaald naar de gesamplede maximale afvoer bij Keulen (afbeelding 3).
- De kritieke waterstand. De kritieke waterstand geeft aan op welk moment een dijk faalt en begint door te breken. Aangezien het, vanwege modelcomplexiteit, onmogelijk is om elke dijksectie mee te nemen als potentiële dijkdoorbraaklocatie, focust deze studie zich enkel op de dijkdoorbraaklocaties die tot grote overstromingen leiden. Deze locaties zorgen dus voor een grote afname van de afvoer in benedenstroomse richting. In totaal zijn 33 dijkdoorbraaklocaties meegenomen in de analyse. Voor de Nederlandse dijken geldt dat deze kunnen falen als gevolg van de faalmechanismes golfoverslag en overloop, piping en macro-stabiliteit. De Duitse dijken kunnen door hun bredere kruin in het model enkel falen ten gevolge van golfoverslag en overloop [7]. De kritieke waterstanden zijn gebaseerd op fragiliteitscurves [8]. Deze curves geven de kans op falen als gevolg van een bepaalde waterstand en bepalen dus de timing van de dijkdoorbraken.
- De dijkdoorbraakbreedte. De uiteindelijke breedte van een dijkdoorbraak is sterk afhankelijk van de opbouw van de dijk en de hydraulische randvoorwaarden. Daarom is deze parameter erg onzeker. In de Monte Carlo-analyse wordt voor elke dijkdoorbraak een breedte willekeurig getrokken. De waardes die gesampled kunnen worden zijn gebaseerd op data van historische dijkdoorbraken.
- De duur van de dijkdoorbraak. Net als de uiteindelijke dijkdoorbraakbreedte, is ook de duur totdat de dijkdoorbraak volledig ontwikkeld is erg onzeker. Ook deze parameter is gebaseerd op data van historische dijkdoorbraken
Om een Monte Carlorun uit te voeren, wordt allereerst een maximale bovenstroomse afvoer gesampled (afbeelding 3). Daarna wordt een golfvorm gesampled en wordt deze geschaald naar de maximale afvoer.
Dit vormt de bovenstroomse randvoorwaarde van het model. Vervolgens wordt voor elk van de 33 dijkdoorbraaklocaties een kritieke waterstand, dijkdoorbraakbreedte en duur van de dijkdoorbraak gesampled. Voor elke tijdstap wordt geëvalueerd of de gesimuleerde waterstanden de kritieke waterstanden overschrijden. Als dit het geval is, begint de dijk door te breken.

Afbeelding 3. Stappen in de Monte Carlo-analyse
De Monte Carlo-analyse resulteert in een afvoer bij Lobith en bijbehorende 95%-betrouwbaarheidsinterval als gevolg van de onzekere random input parameters. De Monte Carlo-analyse is uitgevoerd voor elk van de twaalf historische overstromingen. De resultaten zijn weergegeven in afbeelding 4. Aangezien de afvoeren bij Keulen onzeker zijn, zijn ook bijbehorende afvoeren bij Lobith onzeker.
Afbeelding 4 laat zien dat de afvoer bij Keulen van 1374 enorm afneemt in benedenstroomse richting. Dit komt door dijkdoorbraken en overstromingen die optreden langs de Niederrhein op het traject tussen Keulen en Lobith.
De afvoer bij Keulen was in 1374 met tussen de 18.800 en 29.000 m3/s aanzienlijk groter dan de huidige afvoercapaciteit van de Niederrhein. De overige historische afvoeren waren lager dan deze afvoercapaciteit. Daarom is in de meeste gevallen (b.v. 1496, 1552) de afvoer bij Lobith hoger dan bij Keulen, als gevolg van de toestromingen van de zijrivieren Sieg, Roer en Lippe. In een enkel geval vinden we een afname door dijkdoorbraken (bv. 1651).
De resultaten laten duidelijk zien dat de afvoer bij Lobith niet bepaald kan worden met behulp van een simpele lineaire regressieanalyse van de afvoer bij Keulen. Dit motiveert het gebruik van een hydraulisch model om de huidige gevolgen van de historische overstromingen in kaart te brengen.
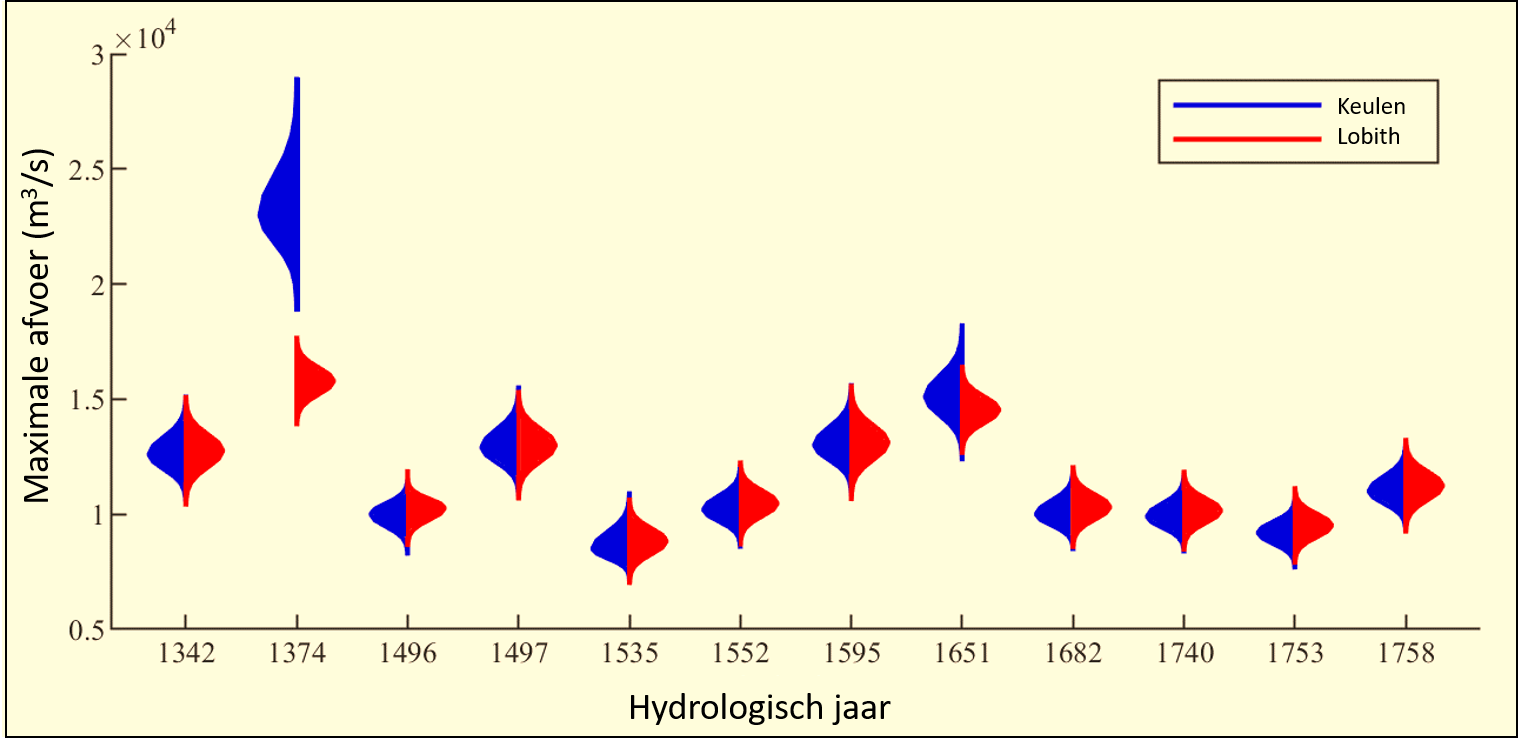
Afbeelding 4. Historische afvoeren bij Keulen en bijbehorende huidige afvoeren bij Lobith
Creëren continue reeks
Als de dataset van jaarlijkse maximale afvoeren voor de periode 1772-2018 wordt uitgebreid met de twaalf historische overstromingen, ontstaat geen continue reeks. Om toch een traditionele overstromingsfrequentieanalyse uit te kunnen voeren, is een continue reeks noodzakelijk. Daarom is een bootstrapmethode gebruikt waarbij de jaarlijkse maximale afvoeren in de periode 1772-2018 worden gesampled over de historische periodes tussen de overstromingen waarvoor geen data beschikbaar is.
Om deze samplingtechniek uit te kunnen voeren, moet een aanname worden gedaan over de perceptiedrempel in de historische periode. De perceptiedrempel geeft aan vanaf welke afvoer de hoogwaters opgemerkt werden als dusdanig ernstig dat er over geschreven of geschilderd werd of dat op een andere manier de ernst van de overstroming genoteerd werd.
In deze studie is de perceptiedrempel gelijkgesteld aan de laagste maximale afvoer van de twaalf historische overstromingen [9]. We nemen aan dat als er een hoogwater had opgetreden met een afvoer hoger dan deze laagste maximale afvoer, hier informatie over beschikbaar zou zijn. Van de dataset 1772-2018 worden alle jaarlijkse maximale afvoeren geselecteerd die lager zijn dan de gekozen perceptiedrempel.
Deze afvoeren zijn gebruikt om de ontbrekende jaren in de historische periode te samplen op basis van ‘trekken met terugleggen’. Voor elk ontbrekend jaar in de historische periode wordt dus willekeurig een afvoer getrokken uit de dataset 1772-2018, waarbij de getrokken afvoer lager is dan de perceptiedrempel. Deze bootstrapmethode resulteert in een continue dataset voor de jaren ca.1300-2018.
Resultaten
Er is een overstromingsfrequentieanalyse uitgevoerd voor zowel de dataset van gemeten jaarlijkse maximale afvoeren voor de periode 1901-2018, als de uitgebreide dataset van de jaren ca.1300-2018. Hierbij wordt de gegeneraliseerde extreme waarde (GEV)-verdeling gebruikt. Deze kansverdeling heeft drie parameters die de locatie, vorm en afvlakking van de curve beïnvloeden. Deze parameters worden gekoppeld met behulp van de methode van de grootste aannemelijke schatter (Maximum Likelihood). Dit is een schattingsmethode die de waarde van de drie parameters kiest waarvoor de gekoppelde curve het beste de onderliggende data weergeeft. De curves voor beide datasets en bijbehorende 95%-betrouwbaarheidsintervallen zijn weergegeven in afbeelding 5.
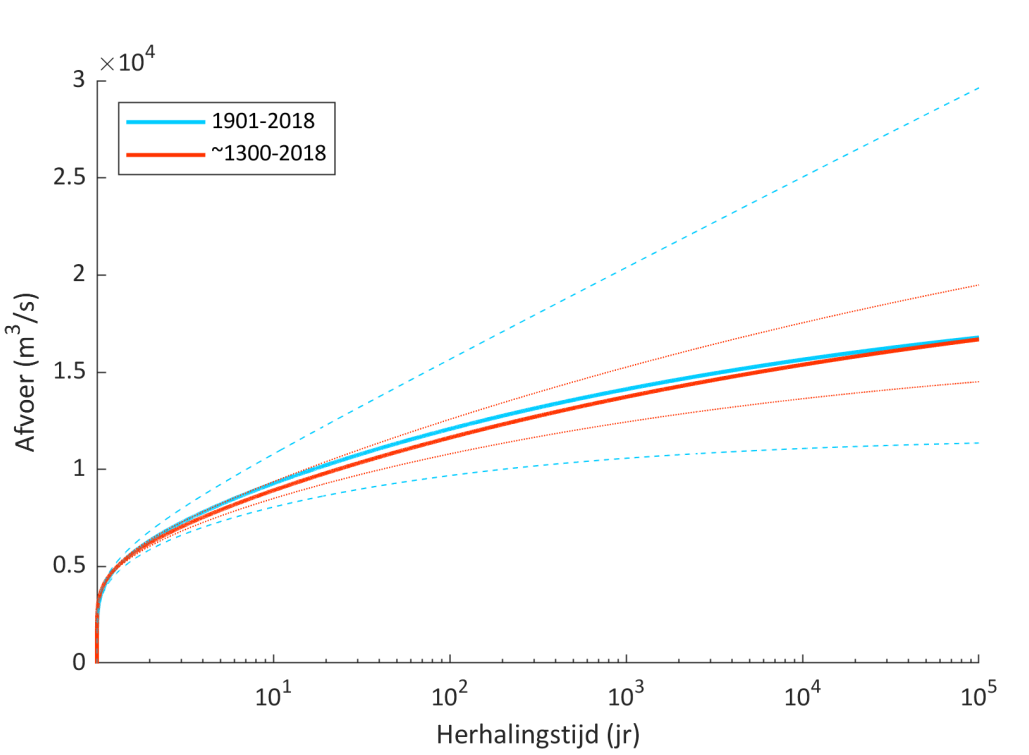
Afbeelding 5. Overstromingsfrequentiecurves voor de gemeten dataset van jaarlijkse maximale afvoeren (1901-2018) en de uitgebreide dataset met historische overstromingen (ca.1300-2018). De stippellijnen geven de corresponderende 95%-betrouwbaarheidsintervallen aan
De ligging van de twee overstromingsfrequentiecurves is nagenoeg hetzelfde. De afvoer die hoort bij een herhalingstijd van 1/100.000 jaar is 16.780 m3/s voor de dataset 1901-2018 en 16.690 m3/s voor de dataset ca.1300-2018. De onzekerheidsbanden verschillen echter aanzienlijk. De breedte van het 95%-betrouwbaarheidsinterval neemt flink af voor de langere datareeks. Dit geldt vooral voor de afvoeren behorende bij extreem hoge herhalingstijden.
Het onzekerheidsinterval van de afvoer voor een herhalingstijd van 1/100.000 jaar neemt maar liefst met 72 procent af. Deze afname is van grote waarde voor beleidsmakers, aangezien met name de bovenrand van het 95%-betrouwbaarheidsinterval kleiner is geworden. Er hoeft dus met minder hoge afvoeren rekening te worden gehouden.
Conclusies en aanbevelingen
In deze studie werd gevonden dat het uitbreiden van de datareeks van jaarlijkse gemeten maximale afvoeren met historische overstromingen de onzekerheid in overstromingsfrequentiecurves significant kan verkleinen. Bij Lobith worden afvoeren gemeten sinds 1901.
Door deze dataset uit te breiden met afvoeren berekend op basis van waterstandmetingen teruggaand tot 1772 [1], en met twaalf genormaliseerde historische overstromingen ontstond een datareeks van ongeveer 700 jaar. Hiermee werd een reductie gevonden van 72 procent in het 95%-betrouwbaarheidsinterval voor de afvoer met een herhalingstijd van 1/100.000 jaar ten opzichte van de traditionele methode.
Geadviseerd wordt dan ook om zoveel mogelijk informatie over historische overstromingen te verzamelen. Deze informatie is te gebruiken om de onzekerheid in overstromingsfrequentiecurves te verkleinen, ook al is de informatie over de historische overstroming zelf erg onzeker. Door het uitbreiden van de datareeks van gemeten afvoeren is vooral de bovenkant van de 95% betrouwbaarheidsinterval afgevlakt, waardoor er met minder hoge afvoeren rekening hoeft te worden gehouden bij het ontwerpen van waterkeringen.
Dankwoord
Dit onderzoek werd ondersteund door het NWO Water2015-programma (Project 14506), dat deels gefinancierd is door het ministerie van Economische Zaken en Klimaat. Daarnaast werd dit onderzoek financieel ondersteund door Rijkswaterstaat en Deltares.
De auteurs willen graag prof. dr. Herget (Universiteit Bonn) en dr. Toonen (KU Leuven) bedanken voor het beschikbaar stellen van de data. Daarnaast willen de auteurs Bas van der Meulen, Kim Cohen en Hans Middelkoop bedanken voor de discussies binnen het project Floods of the Past - Design for the future.
REFERENTIES
1. Toonen, W. H. J. (2015). ‘Flood frequency analysis and discussion of non-stationarity of the Lower Rhine flooding regime (AD1350-2011): Using discharge data, water level measurements, and historical records’. Journal of Hydrology, 528, 490-205. Doi: 10.1016 /j.jhydrol.2015.06.014.
2. Tol, R. D. J., Langen, A. (2000). ‘A concise history of Dutch river floods’. Climatic Change, 46(3), 357-369. Doi: 10.1023/A:1005655412478.
3. Herget, J., Meurs, H. (2010). ‘Reconstructing peak discharges for historic flood levels in the city of Cologne, Germany’. Global and Planetary Change, 70, 108-116. Doi: 10.1016/j.gloplacha.2009.11.011.
4. Kiss, A. (2009). ‘Floods and Weather in 1342 and 1343 in the Carpathian Basin’. Journal of Environmental Geography, 2(3-4), 34-47.
5. Bomers, A., Schielen, R. M. J., Hulscher, S. J. M. H. (2019). 'Consequences of dike breaches and dike overflow in a bifurcating river system’. Natural Hazards. Doi: 10.1007/s11069-019-03643-y
6. Hegnauer, M. et al. (2014). Generator of Rainfall and Discharge Extremes (GRADE) for the Rhine and Meuse basins. Final report of GRADE 2.0. Deltares, Delft, The Netherlands. ISBN: 9789036914062.
7. Apel, H., Merz, B., Thieken, A. H. (2009). ‘Influence of dike breaches on flood frequency estimation.’ Computers & Geosciences 35(5), 907-923. Doi: 10.1016/j.cageo.2007.11.003.
https://www.sciencedirect.com/science/article/pii/S0098300408000265
8. Vuren, S. van et al. (2017). Beleidsstudie Kostenreductie Dijkversterking door Rivierverruiming. Toepassing methodiek op Rijntakken. Consortium Deltares, HKV lijn in Water, Arcadis, Royal HaskoningDHV, Rijkswaterstaat.
9. Bomers, A., Schielen, R. M. J., Hulscher, S. J. M. H. (2019). 'Decreasing uncertainty in flood frequency analyses by including historic flood events in an efficient bootstrap approach'. Natural Hazards and Earth System Sciences, 1895-1908. Doi: 10.5194/nhess-19-1895-2019.



















